在行测数量关系众多行程问题的小考点中,有一个考点只要掌握最终结论,每道题都可以快速地做出来,这个考点就是“直线异地多次相遇”。考点的基本模型是:甲乙两人分别从A、B两地同时出发,不断做往返运动,在该过程中,两人实现多次相遇,行走过程如下图:
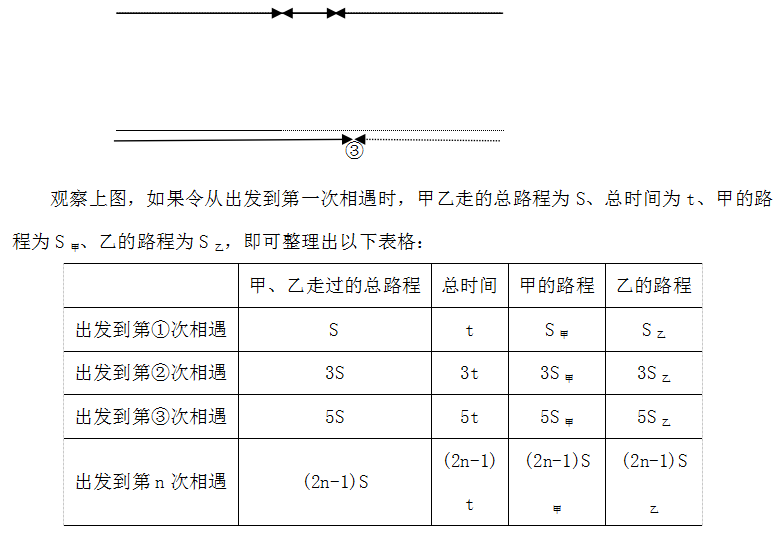
由上表可知,甲乙走过的总路程、总时间、甲的路程、乙的路程存在的比例关系均为1:3:5:……:(2n-1)。知道这个比例关系,就可以解决直线异地多次相遇的所有题目。我们来简单地看两道题:
例1.A、B两地相距160千米。甲、乙两车分别从A、B两地出发,并在两地间不断往返行驶。已知甲车的速度是25km/h,乙车的速度是15km/h。若不计调头时间,30小时内两车迎面相遇了几次?
A.3 B.4 C.5 D.6
解析:从出发到第一次相遇的用时为160÷(25+15)=4小时。设30小时内两车迎面相遇了n次,则由直线异地多次相遇结论可得(2n-1)×4=30,解得n=4.25。所以相遇了4次,选B选项。
例2.甲、乙分别从A、B两地同时出发,匀速相向而行,第一次相遇距A地5米,相遇后继续前进,到达对方起点后立即返回,在距B地3米处第二次相遇,则A、B相距多少米?
A.10
B.12
C.14
D.16
解析:从出发到第一次相遇已知甲的路程为5米,则从出发到第二次相遇甲的路程为5×3米。结合第二次相遇距B地3米可知,甲走的总路程减去3即为A、B两地距离,即5×3-3=12米,选B选项。
(编辑:houmenglin)









